- Poker Starting Hands Odds Calculator Online
- Poker Starting Hands Odds Calculator
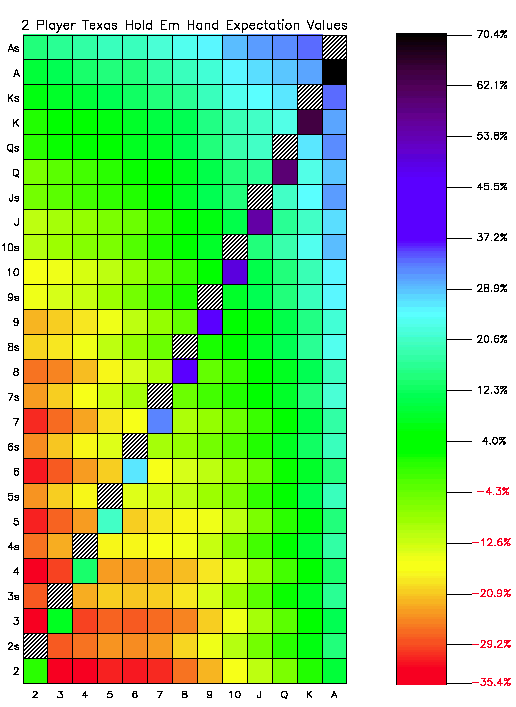
- Poker Starting Hands Odds Calculator Chart
- Poker Starting Hands Odds Calculator 2020
Poker odds charts come in useful when you want to quickly work out the odds of winning a hand in Texas Hold'em. The most commonly used odds charts are the 'standard poker odds charts' below, which give both the percentage and ratio odds of completing your draw depending on the number of outs you have (see pot odds and drawing hands for more information).
Probability of being dealt a certain hand. Probability of being dealt a certain range of hands. A few probability basics. When working out hand probabilities, the main probabilities we will work with are the number of cards in the deck and the number of cards we want to be dealt. So for example, if we were going to deal out 1 card. The Poker Odds Calculator will help you calculate your chances on a given hand, in any situation. One of the most interesting features of the PokerNews Poker Odds Calculator is the guide on the. Poker chips for sale johannesburg. We use 'Rank' to indicate the absolute strength of your starting hand, 1-169, 1 is the best hand. BOL Calculator converts into percentage as 'top%'. BOL Calcuator provides EV, Sklansky Group/Rank and Win Odds for your starting hands. They're all independent numbers. You can choose the one you prefer to play your own starting hands. This is the 5 card poker hands This matches all the hand counts here WIKI poker probabilites. If you are going to write any type of equity calculator, game, or bot this is where I recommend you start. Any simulation needs to be able to identify hands. At 5 cards it is easy with combination.
The second set of odds charts highlight interesting odds for different situations in Texas Hold'em. These will help you get to grips with the different likelihood's and chances within the game of poker.
Standard poker odds charts.
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million).
Other poker odds charts.
Why use these odds charts?
There are currently many odds charts on the Internet at numerous poker websites. However many of these can be tricky to use. ThePokerBank provides easy to use charts highlighting the key draws on each, which makes them simple and effective to use during play.
I am confident that these odds charts are the easiest charts that you will ever use.
How to use poker odds charts.
Poker odds charts help you to determine how much you can call when trying to complete a drawing hand, such as a flush or a straight draw. By comparing your pot odds with the odds of completing your draw, you can work out whether or not it will be profitable to call certain sized bets from your opponents.
Poker odds charts are most commonly used when working out pot odds.
It is perfectly possible to work out the odds of completing a draw in your head, but these odds charts make things much easier if you are looking for a quick reference or if you're just starting out. However, over time it is a good idea to learn the most common odds so that you no longer have to refer to any charts whilst you play.
Work out probabilities for yourself.
Don't just take my word for it or settle for the probabilities I've listed on the site, try working out probabilities for yourself. It's not as tricky or mathsy as you might think.
My guide on how to work out preflop hand probabilities gives a nice overview on basic starting hand probabilities. For flop probabilities and the likelihood of different combinations of cards on the flop, try the article on working out flop probabilities.
Go back to the handy Texas Hold'em tools.
Ever wondered where some of those odds in the odds charts came from? In this article, I will teach you how to work out the probability of being dealt different types of preflop hands in Texas Holdem.
It's all pretty simple and you don't need to be a mathematician to work out the probabilities. I'll keep the math part as straightforward as I can to help keep this an easy-going article for the both of us. Route 66 casino buffet.
- Probability calculations quick links.
A few probability basics.
When working out hand probabilities, the main probabilities we will work with are the number of cards in the deck and the number of cards we want to be dealt. So for example, if we were going to deal out 1 card:
- The probability of dealing a 7 would be 1/52 - There is one 7 in a deck of 52 cards.
- The probability of dealing any Ace would be 4/52 - There four Aces in a deck of 52 cards.
- The probability of dealing any would be 13/52 - There are 13 s in a deck of 52 cards.
In fact, the probability of being dealt any random card (not just the 7) would be 1/52. This also applies to the probability being dealt any random value of card like Kings, tens, fours, whatever (4/52) and the probability of being dealt any random suit (13/52).
Each card is just as likely to be dealt as any other - no special priorities in this game!
The numbers change for future cards.
A quick example.. let's say we want to work out the probability of being dealt a pair of sevens.
- The probability of being dealt a 7 for the first card will be 4/52.
- The probability of being dealt a 7 for the second card will be 3/51.
Notice how the probability changes for the second card? After we have been dealt the first card, there is now 1 less card in the deck making it 51 cards in total. Also, after already being dealt a 7, there are now only three 7s left in the deck.
Always try and take care with the numbers for future cards. The numbers will change slightly as you go along.
Working out probabilities.
- Whenever the word 'and' is used, it will usually mean multiply.
- Whenever the word 'or' is used, it will usually mean add.
This won't make much sense for now, but it will make a lot of sense a little further on in the article. Trust me.
Probability of being dealt two exact cards.
Multiply the two probabilities together.
So, we want to find the probability of being dealt the A and K. (See the 'and' there?)
- Probability of being dealt A - 1/52.
- Probability of being dealt K - 1/51.
Now let's just multiply these bad boys together.
P = (1/52) * (1/51)
P = 1/2652
So the probability of being dealt the A and then K is 1/2652. As you might be able to work out, this is the same probability for any two exact cards, as the likelihood of being dealt A K is the same as being dealt a hand like 7 3 in that order.
But wait, we do not care about the order of the cards we are dealt!
When we are dealt a hand in Texas Hold'em, we don't care whether we get the A first or the K first (which is what we just worked out), just as long as we get them in our hand it's all the same. There are two possible combinations of being dealt this hand (A K and K A), so we simply multiply the probability by 2 to get a more useful probability.
P = 1/2652 * 2
P = 1/1326
You might notice that because of this, we have also worked out that there are 1,326 possible combinations of starting hands in Texas Holdem. Cool huh?
Probability of being dealt a certain hand.
Two exact cards is all well and good, but what if we want to work out the chances of being dealt AK, regardless of specific suits and whatnot? Well, we just do the same again..
Multiply the two probabilities together.
So, we want to find the probability of being dealt any Ace andany King.
- Probability of being dealt any Ace - 4/52.
- Probability of being dealt any King - 4/51 (after we've been dealt our Ace, there are now 51 cards left).
P = (4/52) * (4/51)
P = 16/2652 = 1/166
However, again with the 2652 number we are working out the probability of being deal an Ace and then a King. If we want the probability of being dealt either in any order, there are two possible ways to make this AK combination so we multiply the probability by 2.
P = 16/2652 * 2
P = 32/2652
P = 1/83
The probability of being dealt any AK as opposed to an AK with exact suits is more probable as we would expect. A lot more probable in fact. Also, as you might guess, this probability of 1/83 will be the same for any two value of cards like; AQ, JT, 34, J2 and so on regardless of whether they are suited or not.
Probability of being dealt a range of hands.
Work out each individual hand probability and add them together.
What's the probability of being dealt AA or KK? (Spot the 'or' there? - Time to add.)
- Probability of being dealt AA - 1/221 (4/52 * 3/51 = 1/221).
- Probability of being dealt KK - 1/221 (4/52 * 3/51 = 1/221).
P = (1/221) + (1/221)
P = 2/221 = 1/110
Easy enough. If you want to add more possible hands in to the range, just work out their individual probability and add them in. So if we wanted to work out the odds of being dealt AA, KK or 7 3..
- Probability of being dealt AA - 1/221 (4/52 * 3/51 = 1/221).
- Probability of being dealt KK - 1/221 (4/52 * 3/51 = 1/221).
- Probability of being dealt 7 3 - 1/1326 ([1/52 * 1/51] * 2 = 1/1326).
P = (1/221) + (1/221) + (1/1326)
P = 359/36465 = 1/102
Poker Starting Hands Odds Calculator Online
This one definitely takes more skill with adding fractions because of the different denominators, but you get the idea. I'm just teaching hand probabilities here, so I'm not going to go in to adding fractions in this article for now! This fractions calculator is really handy for adding those trickier probabilities quickly though.
Overview of working out hand probabilities.
Hopefully that's enough information and examples to allow you to go off and work out the probabilities of being dealt various hands and ranges of hands before the flop in Texas Holdem. The best way to learn how to work out probabilities is to actually try and work it out for yourself, otherwise the maths part will just go in one ear and out the other.
I guess this article isn't really going to do much for improving your game, but it's still pretty interesting to know the odds of being dealt different types of hands.
Poker Starting Hands Odds Calculator

How to use poker odds charts.
Poker odds charts help you to determine how much you can call when trying to complete a drawing hand, such as a flush or a straight draw. By comparing your pot odds with the odds of completing your draw, you can work out whether or not it will be profitable to call certain sized bets from your opponents.
Poker odds charts are most commonly used when working out pot odds.
It is perfectly possible to work out the odds of completing a draw in your head, but these odds charts make things much easier if you are looking for a quick reference or if you're just starting out. However, over time it is a good idea to learn the most common odds so that you no longer have to refer to any charts whilst you play.
Work out probabilities for yourself.
Don't just take my word for it or settle for the probabilities I've listed on the site, try working out probabilities for yourself. It's not as tricky or mathsy as you might think.
My guide on how to work out preflop hand probabilities gives a nice overview on basic starting hand probabilities. For flop probabilities and the likelihood of different combinations of cards on the flop, try the article on working out flop probabilities.
Go back to the handy Texas Hold'em tools.
Ever wondered where some of those odds in the odds charts came from? In this article, I will teach you how to work out the probability of being dealt different types of preflop hands in Texas Holdem.
It's all pretty simple and you don't need to be a mathematician to work out the probabilities. I'll keep the math part as straightforward as I can to help keep this an easy-going article for the both of us. Route 66 casino buffet.
- Probability calculations quick links.
A few probability basics.
When working out hand probabilities, the main probabilities we will work with are the number of cards in the deck and the number of cards we want to be dealt. So for example, if we were going to deal out 1 card:
- The probability of dealing a 7 would be 1/52 - There is one 7 in a deck of 52 cards.
- The probability of dealing any Ace would be 4/52 - There four Aces in a deck of 52 cards.
- The probability of dealing any would be 13/52 - There are 13 s in a deck of 52 cards.
In fact, the probability of being dealt any random card (not just the 7) would be 1/52. This also applies to the probability being dealt any random value of card like Kings, tens, fours, whatever (4/52) and the probability of being dealt any random suit (13/52).
Each card is just as likely to be dealt as any other - no special priorities in this game!
The numbers change for future cards.
A quick example.. let's say we want to work out the probability of being dealt a pair of sevens.
- The probability of being dealt a 7 for the first card will be 4/52.
- The probability of being dealt a 7 for the second card will be 3/51.
Notice how the probability changes for the second card? After we have been dealt the first card, there is now 1 less card in the deck making it 51 cards in total. Also, after already being dealt a 7, there are now only three 7s left in the deck.
Always try and take care with the numbers for future cards. The numbers will change slightly as you go along.
Working out probabilities.
- Whenever the word 'and' is used, it will usually mean multiply.
- Whenever the word 'or' is used, it will usually mean add.
This won't make much sense for now, but it will make a lot of sense a little further on in the article. Trust me.
Probability of being dealt two exact cards.
Multiply the two probabilities together.
So, we want to find the probability of being dealt the A and K. (See the 'and' there?)
- Probability of being dealt A - 1/52.
- Probability of being dealt K - 1/51.
Now let's just multiply these bad boys together.
P = (1/52) * (1/51)
P = 1/2652
So the probability of being dealt the A and then K is 1/2652. As you might be able to work out, this is the same probability for any two exact cards, as the likelihood of being dealt A K is the same as being dealt a hand like 7 3 in that order.
But wait, we do not care about the order of the cards we are dealt!
When we are dealt a hand in Texas Hold'em, we don't care whether we get the A first or the K first (which is what we just worked out), just as long as we get them in our hand it's all the same. There are two possible combinations of being dealt this hand (A K and K A), so we simply multiply the probability by 2 to get a more useful probability.
P = 1/2652 * 2
P = 1/1326
You might notice that because of this, we have also worked out that there are 1,326 possible combinations of starting hands in Texas Holdem. Cool huh?
Probability of being dealt a certain hand.
Two exact cards is all well and good, but what if we want to work out the chances of being dealt AK, regardless of specific suits and whatnot? Well, we just do the same again..
Multiply the two probabilities together.
So, we want to find the probability of being dealt any Ace andany King.
- Probability of being dealt any Ace - 4/52.
- Probability of being dealt any King - 4/51 (after we've been dealt our Ace, there are now 51 cards left).
P = (4/52) * (4/51)
P = 16/2652 = 1/166
However, again with the 2652 number we are working out the probability of being deal an Ace and then a King. If we want the probability of being dealt either in any order, there are two possible ways to make this AK combination so we multiply the probability by 2.
P = 16/2652 * 2
P = 32/2652
P = 1/83
The probability of being dealt any AK as opposed to an AK with exact suits is more probable as we would expect. A lot more probable in fact. Also, as you might guess, this probability of 1/83 will be the same for any two value of cards like; AQ, JT, 34, J2 and so on regardless of whether they are suited or not.
Probability of being dealt a range of hands.
Work out each individual hand probability and add them together.
What's the probability of being dealt AA or KK? (Spot the 'or' there? - Time to add.)
- Probability of being dealt AA - 1/221 (4/52 * 3/51 = 1/221).
- Probability of being dealt KK - 1/221 (4/52 * 3/51 = 1/221).
P = (1/221) + (1/221)
P = 2/221 = 1/110
Easy enough. If you want to add more possible hands in to the range, just work out their individual probability and add them in. So if we wanted to work out the odds of being dealt AA, KK or 7 3..
- Probability of being dealt AA - 1/221 (4/52 * 3/51 = 1/221).
- Probability of being dealt KK - 1/221 (4/52 * 3/51 = 1/221).
- Probability of being dealt 7 3 - 1/1326 ([1/52 * 1/51] * 2 = 1/1326).
P = (1/221) + (1/221) + (1/1326)
P = 359/36465 = 1/102
Poker Starting Hands Odds Calculator Online
This one definitely takes more skill with adding fractions because of the different denominators, but you get the idea. I'm just teaching hand probabilities here, so I'm not going to go in to adding fractions in this article for now! This fractions calculator is really handy for adding those trickier probabilities quickly though.
Overview of working out hand probabilities.
Hopefully that's enough information and examples to allow you to go off and work out the probabilities of being dealt various hands and ranges of hands before the flop in Texas Holdem. The best way to learn how to work out probabilities is to actually try and work it out for yourself, otherwise the maths part will just go in one ear and out the other.
I guess this article isn't really going to do much for improving your game, but it's still pretty interesting to know the odds of being dealt different types of hands.
Poker Starting Hands Odds Calculator
I'm sure that some of you reading this article were not aware that the probability of being dealt AA were exactly the same as the probability of being dealt 22! Well, now you know - it's 1/221.
Other useful articles.
- Poker mathematics.
- Pot odds.
- Equity in poker.
Go back to the poker odds charts.
Can You Afford Not To Use
Poker Tracker 4?
'I wouldn't play another session of online poker without it'
Poker Starting Hands Odds Calculator Chart
'I play $25NL, and in under 1 week PT4 had paid for itself'
Poker Starting Hands Odds Calculator 2020
Comments